15 UNICENTRO 2020 :
B) x + y – √3 = 0
C) y – √3x + 1 = 0
Solução comentada:
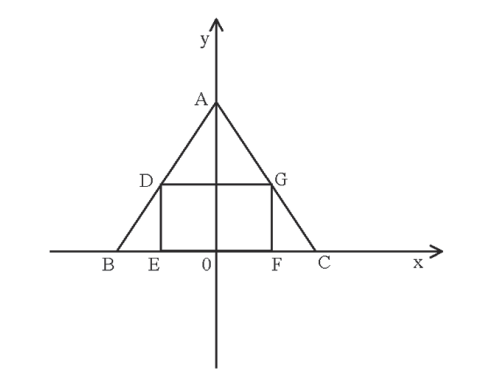
Temos claramente um exercício envolvendo geometria plana, equação e função de 1º grau.
O comando do exercício é: pode-se afirmar que a reta AC tem equação cartesiana da forma.
Logo, queremos saber a equação da reta AC.
Sabemos que uma equação de reta será dada por:
y=ax+b
Sabemos que o triângulo é equilátero e tem lado dois, portanto temos que:
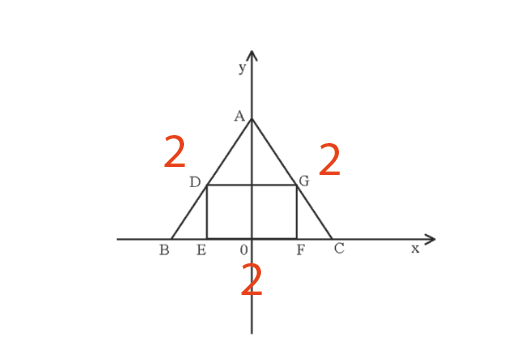
Para encontrarmos a equação, podemos iniciar encontrando b. Sabemos que b é o ponto que cruza o eixo y. Logo no caso do exercício esse valor será dado pela altura do triângulo, que pode ser encontrado através de Pitágoras:
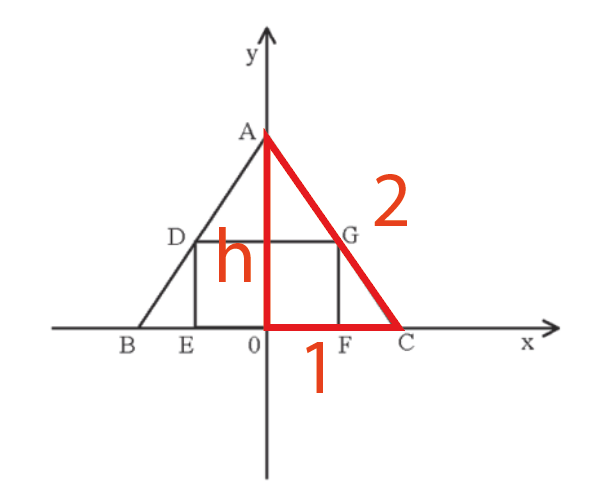
b=h=\sqrt{2^2-1^2}\\
\ \\
b=\sqrt{3}Podemos encontrar o valor de a identificando que a raiz da equação é 1:
0=1*a+\sqrt{3}\\
\ \\
a=-\sqrt{3}Logo, temos que a equação será dada por:
y=-\sqrt{3}x+\sqrt{3}\\
\ \\
\sqrt{3}x+y-\sqrt{3}=0A alternativa que nos trás esta equação é a letra D.
GABARITO 15 UNICENTRO 2020 : D.
Confira a resolução de todos os exercícios do Unicentro.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.





