8 UNICENTRO 2021 – A prefeitura de uma determinada cidade

8 UNICENTRO 2021 :

8 UNICENTRO 2021 ) A prefeitura de uma determinada cidade decidiu aproveitar garrafas PET para montar uma árvore de natal bem grande, bonita e de baixo custo, num formato triangular, cuja base terá 1024 garrafas e no topo apenas uma. O número de garrafas, por fileira, decresce da base para o topo conforme uma progressão geométrica de razão 1/2.

Com base nessas informações e desconsiderando quaisquer outros adereços, assinale a alternativa que apresenta, corretamente, o número de garrafas PET necessário para a construção desta árvore de natal.

a) 1024

b) 1983

c) 1984

d) 2047

e) 2048

Confira abaixo a resolução completa:

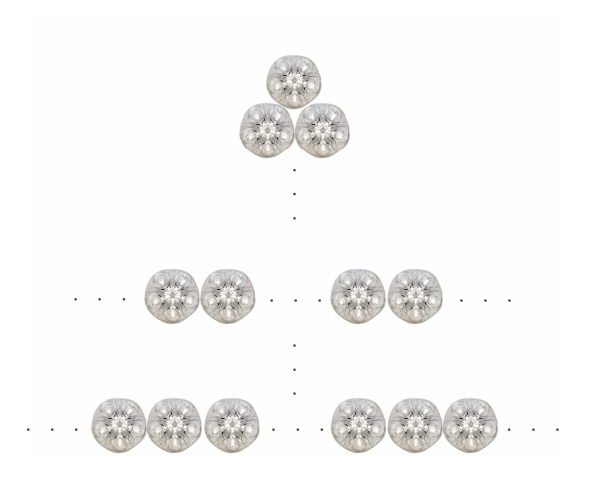
Solução comentada:

Temos claramente um exercício envolvendo progressão geométrica.

O comando deste exercício é: Com base nessas informações e desconsiderando quaisquer outros adereços, assinale a alternativa que apresenta, corretamente, o número de garrafas PET necessário para a construção desta árvore de natal.

Logo, em outras palavras, o exercício quer saber a soma dos n termos da PG.

Sabemos que a soma de n termos de uma PG é dada por:

S_n=\frac{a_1*(q^n-1)}{q-1}

Segundo o enunciado temos algumas informações para calcular a soma total:

• progressão geométrica de razão 1/2, logo q=1/2;
• base terá 1024 garrafas e no topo apenas uma, sendo assim a₁=1024 e a_n=1.

Então, para calcularmos a soma basta encontrar o número de termos n.

Para isso podemos utilizar a equação geral de uma PG:

a_n=a_1*q^{n-1}\\
\ \\
1=1024*(\frac{1}{2})^{n-1}\\
\ \\
\frac{1}{1024}=(\frac{1}{2})^{n-1}\\

Sabemos que 2¹⁰=1024, e que todo expoente em base 1 é igual a 1, logo:

\frac{1}{1024}=(\frac{1}{2})^{n-1}\\
\ \\
\frac{1}{2^{10}}=\frac{1}{2^{n-1}}\\
\ \\
Sendo\ assim:\\
\ \\
2^{-10}=2^{-(n-1)}\\
\ \\
-10=-n+1\\
 \ \\
n=11

Sendo assim, substituindo todos os valores no termo geral da soma de uma PG:

S_{11}=\frac{1024*((\frac{1}{2})^11-1)}{\frac{1}{2}-1}\\
\ \\
S_{11}=\frac{1024*(\frac{1}{2048}-1)}{-\frac{1}{2}}\\
\ \\
S_{11}=\frac{1024*(-\frac{2047}{2048})}{-\frac{1}{2}}\\
\ \\
S_{11}=(-2)*1024*(-\frac{2047}{2048})\\
\ \\
S_{11}=2047\ \\

Portanto a alternativa que nos trás esta soma é a alternativa D.

GABARITO 8 UNICENTRO 2021 : D.

Confira a resolução de todos os exercícios do Unicentro.

Confira aqui mais resoluções no site.

Quer tirar mais de 700 em Matemática no Enem?

Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:

• Muito mais organizada;
• Mais rápida;
• Economizando contas;
• Analisando os exercícios.

Adquira já o seu aqui.