5 UNICENTRO 2021 :
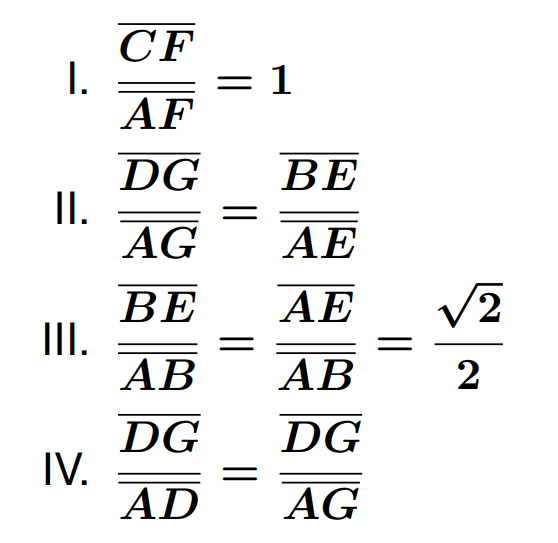
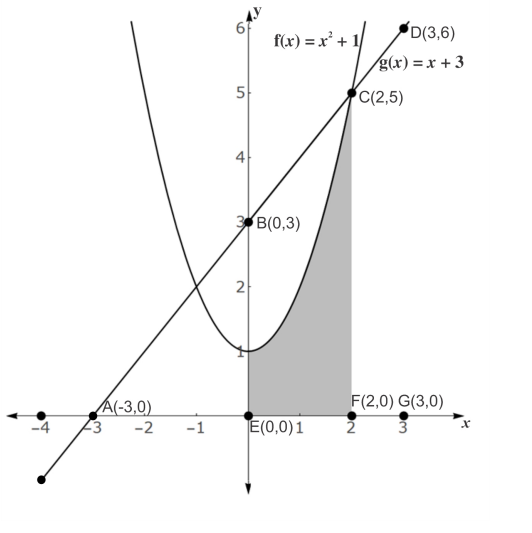
Assinale a alternativa correta.
Solução comentada:
Temos claramente um exercício envolvendo geometria espacial.
Nesse exercício vamos ter que verificar cada uma das afirmativas para verificar quais estão corretas.
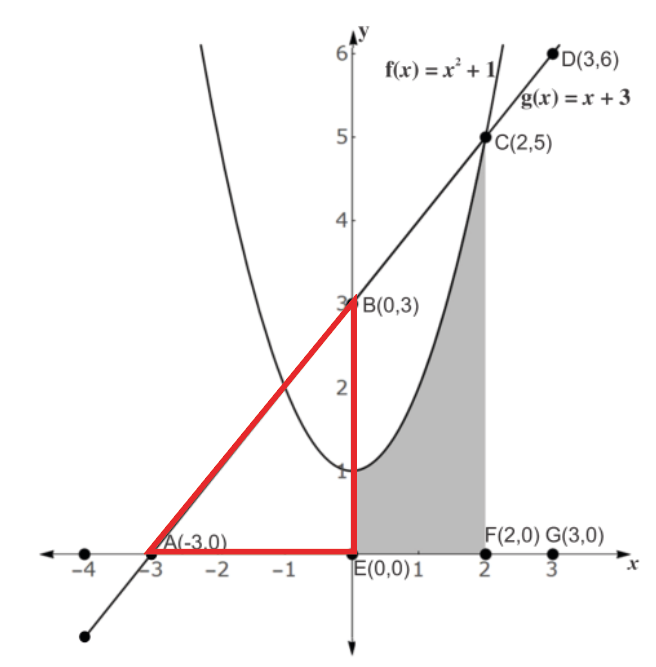
1. CF/AF=1.
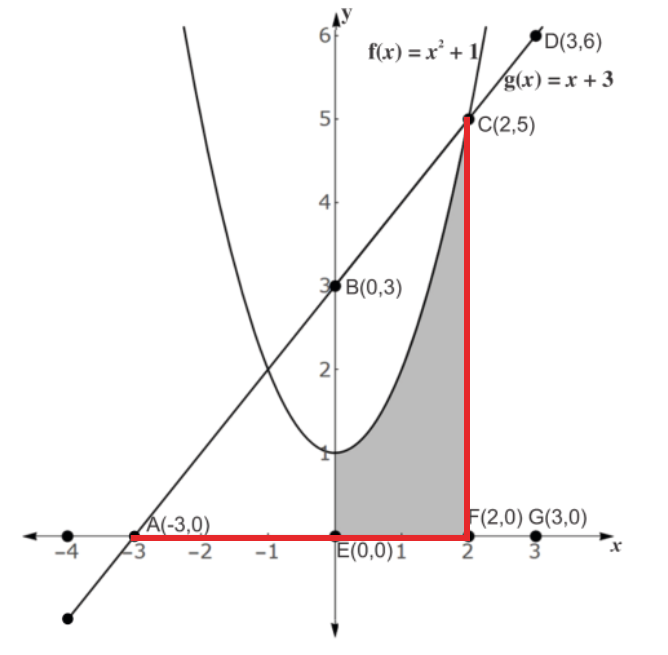
Observando o gráfico temos que:
- CF = 5-0=5;
- AF = 2-(-3)=5.
Sendo assim:
\frac{CF}{AF}=\frac{5}{5}=1Sendo assim a 1 é VERDADEIRA.
2. DG/AG=BE/AE.
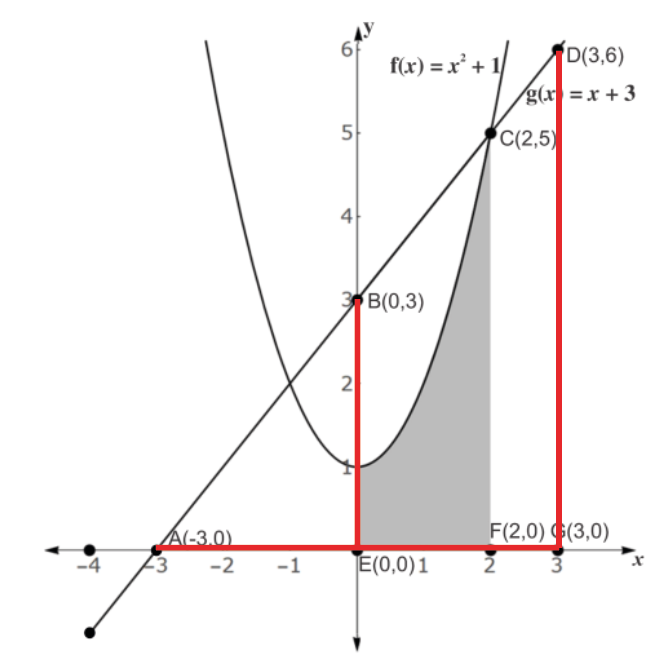
Observando o gráfico temos que:
- DG=6-0=6;
- AG=3-(-3)=6;
- BE=3-0=3;
- AE=0-(-3)=3.
Sendo assim:
\frac{DG}{AG}=\frac{BE}{AE}\\
\ \\
\frac{6}{6}=\frac{3}{3}\\
\ \\
1=1Sendo assim a 2 é VERDADEIRA.
3. BE/AB=AE/AB=√2/2
Observando o gráfico temos os simples:
- AE=0-(-3)=3;
- BE=3-0=3.
Para calcular AB vamos utilizar de Pitágoras pois é um triângulo retângulo:
AB^2=AE^2+BE^2\\
\ \\
AB=\sqrt{3^2+3^2}\\
\ \\
AB=\sqrt{2*3^2}\\
\ \\
AB=3\sqrt{2}\\Sendo assim:
\frac{BE}{AB}=\frac{AE}{AB}\\
\ \\
\frac{3}{3\sqrt{2}}=\frac{3}{3\sqrt{2}}\\
\ \\
\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{2}}\\
\ \\
\frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{2}\\Sendo assim a igualdade é válida e a 3 é VERDADEIRA.
4. DG/AD=DG/AG.
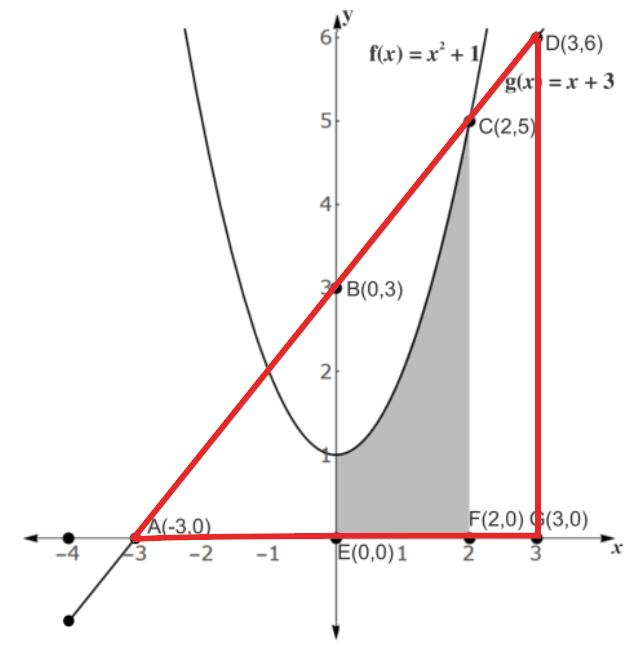
Observando o gráfico temos os simples:
- DG=6-0=6;
- AG=3-(-3)=6.
Para encontrar AD também podemos fazer por Pitágoras:
AD^2=AG^2+DG^2\\
\ \\
AD=\sqrt{6^2+6^2}\\
\ \\
AD=\sqrt{2*6^2}\\
\ \\
AD=6\sqrt{2}\\
\ \\Sendo assim, vamos verificar:
\frac{DG}{AD}=\frac{DG}{AG}\\
\ \\
\frac{6}{6\sqrt{2}} \neq \frac{6}{6}\\
\ \\Logo, não são iguais, e sim diferentes.
Sendo assim a 4 é FALSA.
Logo as corretas são a 1, 2 e 3.
GABARITO 5 UNICENTRO 2021 : D.
Confira a resolução de todos os exercícios do Unicentro.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.





