3 UNICENTRO 2021 – Com base no gráfico, atribua V (verdadeiro) ou F (falso) às afirmativas a seguir

3 UNICENTRO 2021 :

3 UNICENTRO 2021 ) Com base no gráfico, atribua V (verdadeiro) ou F (falso) às afirmativas a seguir.
( ) A distância entre os pontos A(−4, g(−4)) e C(2, f(2)) é 6√2 u.m.
( ) Existe x ∈ dom(f) tal que f(x) = 0.
( ) Para todo x no intervalo [−1, 2], vale que g(x) ≥ f(x).
( ) As retas de equações y = −2x + 3 e y = x + 3 são perpendiculares.
( ) dom(f)∩dom(g) = {0}
Assinale a alternativa que contém, de cima para baixo, a sequência correta.

a) V, V, F, F, F.

b) V, F, V, F, F.

c) V, F, F, V, F.

d) F, V, V, F, V.

e) F, F, V, V, V

Confira abaixo a resolução completa:

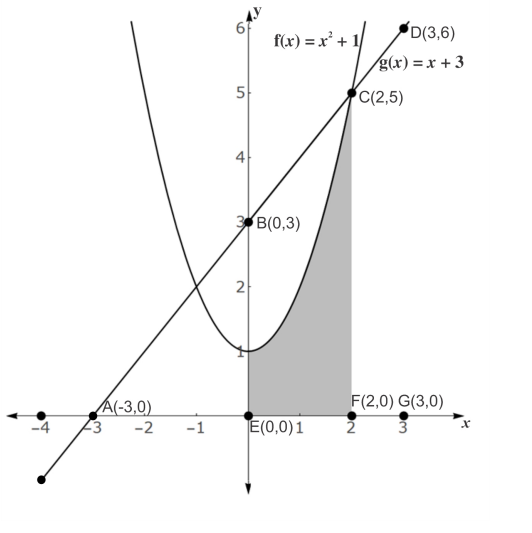
Solução comentada:

Temos claramente um exercício envolvendo funções de 2º grau.

Temos 5 sentenças onde precisamos verificar se as afirmações são verdadeiras ou falsas. Então vamos lá:

( ) A distância entre os pontos A(−4, g(−4)) e C(2, f(2)) é 6√2 u.m.

Primeiramente vamos calcular quem são os pontos A e C.

PONTO A:

A(-4, g(-4))\\
\ \\
g(-4)=-4+3=-1\\
\ \\
A(-4, -1).

PONTO C:

C(2, f(2))\\
\ \\
f(2)=2^2+1=5\\
\ \\
C(2, 5)

Para calcular a distância basta utilizar de teorema de Pitágoras com as distâncias em x e em y:

Distância em x: 2+4=6.

Distância em y: 5+1=6.

Sendo assim:

d=\sqrt{6^2+6^2}=\sqrt{2*6^2}=6\sqrt{2}

Logo, é VERDADEIRO, uma vez que o resultado da distância está correto.

( ) Existe x ∈ dom(f) tal que f(x) = 0.

FALSO. Pois a função f(x) não cruza o eixo das abcissas. Sendo assim não possui raízes reais.

( ) Para todo x no intervalo [−1, 2], vale que g(x) ≥ f(x).

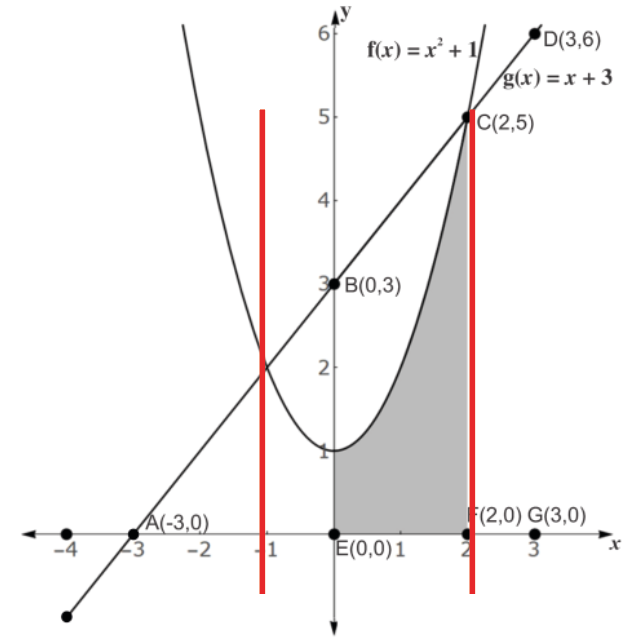
VERDADEIRO. Como no intervalo [-1,2] a função g(x) está acima do gráfico da função f(x) podemos afirmar que esta correta.

( ) As retas de equações y = −2x + 3 e y = x + 3 são perpendiculares.

Para que duas retas sejam perpendiculares os coeficientes angulares devem ser opostos. Logo, temos que:

m_2=-\frac{1}{m_1}

Nesse caso temos que m1=-2, logo o coeficiente da reta perpendicular será:

m_2=-\frac{1}{m_1}\\
\ \\
m_2=-\frac{1}{-2}\\
\ \\
m_2=\frac{1}{2}\\

Como o coeficiente da segunda reta y = x + 3 é 1, confirmamos que não é igual.

Portanto é FALSA. Pois não são perpendiculares.

( ) dom(f)∩dom(g) = {0}

FALSO, pois o domínio de f está contido no domínio de g, uma vez que ambos os domínios são o conjunto dos REAIS.

Logo a sequência será: V, F, V, F, F.

GABARITO 3 UNICENTRO 2021 : B.

Confira a resolução de todos os exercícios do Unicentro.

Confira aqui mais resoluções no site.

Quer tirar mais de 700 em Matemática no Enem?

Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:

• Muito mais organizada;
• Mais rápida;
• Economizando contas;
• Analisando os exercícios.

Adquira já o seu aqui.