32 UEPG 2019 VERÃO:
32 UEPG 2019 VERÃO) Sabendo que “a” representa a solução da equação
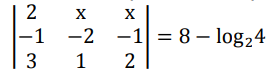
, assinale o que for correto.
01) Se f(x) = ax + 2 e g(x) = x² então f(g(x)) = 0 não admite raízes reais.
02) A solução da equação log6(x² − x) = 1 é S = {-2, a}.
04) A solução da equação exponencial 5^x =1/125 é S = {-a}.
08) A soma dos coeficientes dos termos do binômio (x + a)^4 é 16.
Solução comentada:
Temos claramente um exercício envolvendo funções de primeiro e segundo grau, logaritmo e equações exponenciais.
Para resolver as sentenças primeiro precisamos encontrar o valor de a.
Podemos encontrar a através do determinante da matriz igual ao logaritmo.
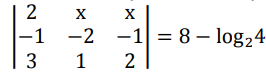
Para solucionar primeira coisa que precisamos saber é:
log_24=2
Sendo assim, temos:
8-2=6.
Logo o determinante da matriz será igual a 6.
Sendo assim vamos solucionar, calculando o determinante e igualando a 6:
-8-3x-x-(-6x-2-2x)=6\\ \ \\ 4x=12\\ \ \\ x=3\\ \ \\ Logo:\\ \ \\ a=3
Sabendo que a vale 12 vamos para as sentenças.
01) Se f(x) = ax + 2 e g(x) = x² então f(g(x)) = 0 não admite raízes reais.
Primeiramente, f(x) é, com o valor de a:
f(x)=3x+2
Substituindo g(x) composto dentro da f(x):
f(g(x))=f(x²)=3x²+2
Para encontrar as raízes igualamos a zero:
3x^2+2=0\\
\ \\
3x^2=-2\\
\ \\
x=\sqrt{\frac{-2}{3}}Como não existe raiz quadrada de número negativo, não temos raízes reais.
Logo a 01 está correta.
02) A solução da equação log6(x² − x) = 1 é S = {-2, a}.
Vamos solucionar a equação. Por propriedades de logaritmos temos que:
x^2-x=6^1\\
\ \\
x^2-x-6=0\\
\ \\
Por\ bhaskara:\\
\ \\
x=\frac{1\pm\sqrt{(-1)^2-4*1*(-6)}}{2*1}=\frac{1\pm\sqrt{25}}{2}=\frac{1\pm5}{2}\\
\ \\
x'=3\\
x''=-2Logo, realmente a solução é S={-2,a}, que no caso é S={-2,3}.
Logo a 02 está correta.
04) A solução da equação exponencial 5^x =1/125 é S = {-a}.
Vamos solucionar esta equação exponencial:
5^x=\frac{1}{125}\\
\ \\
5^x=\frac{1}{5^3}\\
\ \\
5^x=5^{-3}\\
\ \\
x=-3Como a solução é -3, e -3 é -a, está correto.
Logo a 04 está correta.
Logo a 04 está correta.
08) A soma dos coeficientes dos termos do binômio (x + a)^4 é 16.
Substituindo a na expressão, temos que:
(x+3)^4
Para sabermos a soma dos coeficientes, basta sabermos que o coeficiente de x é 1, e somar (1+3)^4. Sendo assim:
(1+3)^4=4^4=16*16
Logo, não é 16, e sim 16².
Logo a 08 está incorreta.
O gabarito da questão é então: 1+2+4=7.
GABARITO 32 UEPG 2019 VERÃO: 7.
Confira a resolução de todos os exercícios do Enem.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.




