34 UEPG 2020 – Sabendo que x deixa resto 4 quando dividido

34 UEPG 2020:

34 UEPG 2020) Sabendo que x deixa resto 4 quando dividido por 8 e y deixa resto 3 quando dividido por 8, assinale o que for correto.

01) x + 3y deixa resto 6 quando dividido por 8.

02) 3y deixa resto 1 quando dividido por 8.

04) x – y deixa resto 7 quando dividido por 8.

08) x + y deixa resto 7 quando dividido por 8.

Confira abaixo a resolução completa:

Solução comentada:

Temos claramente um exercício envolvendo aritmética.

Para encontrar as respostas das alternativas, primeiro precisamos definir quem é x e quem é y.

Sabemos que x pode ser escrito como 8 vezes um quociente a mais o resto 4, por propriedades de divisão, temos então que:

x=8*a+4

Uma vez que a é o quociente da divisão com resto 8:

Para y podemos fazer a mesma coisa, afirmando que y é igual a 8 vezes um quociente b mais o resto 3:

y=8*b+3

Sendo que:

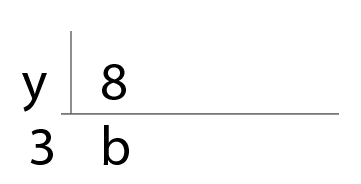
Podemos considerar que:

a=b=1

Sendo assim:

x=8*a+4=8*1+4=12\\
\ \\
x=12\\
\ \\
y=8*b+3=8*1+3=11\\
\ \\
y=11

Sendo assim podemos ir para as sentenças:

01) x + 3y deixa resto 6 quando dividido por 8.

Vamos calcular:

x+3y=12+3*11=45\\
\ \\
\frac{45}{8}=\frac{40}{8}+\frac{5}{8}=5+\frac{5}{8}\\
\ \\

Logo como sobra 5 sem dividir, o resto é 5 e não 6. Sendo assim a 01 está incorreta.

02) 3y deixa resto 1 quando dividido por 8.

Vamos calcular:

3y=3*11=33\\ 
\ \\
\frac{33}{8}=\frac{32}{8}+\frac{1}{8}=4+\frac{1}{8}

Logo como sobra 1 sem dividir, o resto é 1. Sendo assim a 02 está correta.

04) x – y deixa resto 7 quando dividido por 8.

Vamos calcular:

x-y=12-11=1
\ \\
\frac{1}{8}

O resto é 1 e não 7. Sendo assim a 04 está incorreta.

08) x + y deixa resto 7 quando dividido por 8.

Vamos calcular:

x+y=12+11=23\\
\ \\
\frac{23}{8}=\frac{16}{8}+\frac{7}{8}=2+\frac{7}{8}

Logo como sobra 7 sem dividir, o resto é 7. Sendo assim a 08 está correta.

Sendo assim o gabarito é: 2+8=10.

GABARITO 34 UEPG 2020: 10.

Confira a resolução de todos os exercícios do Enem.

Confira aqui mais resoluções no site.

aqui mais resoluções no site.

Quer tirar mais de 700 em Matemática no Enem?

Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:

• Muito mais organizada;
• Mais rápida;
• Economizando contas;
• Analisando os exercícios.

Adquira já o seu aqui.