01. Se as matrizes
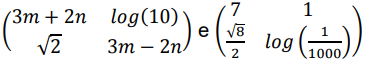
são iguais, então m.n = 5/3.
02. A matriz
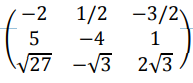
admite inversa.
04.

08. O sistema
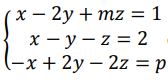
é indeterminado para 𝑚 = 2 𝑒 𝑝 = −1.
16. Se 𝐴 e 𝐵 são matrizes quadradas de mesma ordem, então (𝐴 ∙ 𝐵)^𝑡 = 𝐴^𝑡 ∙ 𝐵^𝑡.
32. Se 𝑥1 e 𝑥2 são raízes da equação 𝑥² + 2𝑥 + 10 = 0, então |𝑥1| + |𝑥2| = 2√10.
Confira abaixo a resolução completa:
Solução comentada:
01. Se as matrizes
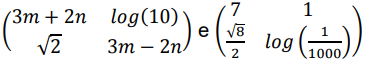
são iguais, então m.n = 5/3.
Como o exercício diz que as matrizes são iguais, para encontrarmos m e n, para no final calcularmos o seu produto, basicamente vamos igualar o elemento a11 da primeira matriz com o elemento a11 da segunda matriz, assim como o elemento a22 da primeira matriz com o elemento a22 da segunda matriz.
Fazemos isso pois esses são os dois elementos que possuem os termos a e m.
Sendo assim:
\begin{cases}
3m+2n=7\\
3m-2n=log(\frac{1}{1000})
\end{cases}\\
Antes de solucionar o sistema de equação, vamos primeiro encontrar qual o valor do logaritmo através de propriedade de logaritmo, sabendo que o log quando não tem a base especificada é log na base 10:
log(\frac{1}{1000})=log(10^{-3)}=-3*log(10)=-3Sendo assim:
\begin{cases}
3m+2n=7\\
3m-2n=-3
\end{cases}\\
Somando\ as\ duas\ equações:\\
\ \\
3m+2n+3m-2n=7-3\\
\ \\
6m=4\\
\ \\
m=\frac{2}{3}\\
\ \\
encontrando\ n\ com\ qualquer\ uma\ das\ duas\ equações:\\
\ \\
3*\frac{2}{3}+2n=7\\
\ \\
2n=7-2\\
\ \\
n=\frac{5}{2}
Sabendo quem são os dois, agora basta calcular o produto:
m*n=\frac{2}{3}*\frac{5}{2}=\frac{5}{3}Sendo assim, como realmente é 5/3 a 01 está correta.
02. A MATRIZ
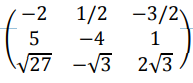
admite inversa.
Para sabermos se uma matriz admite inversa basta calcularmos o determinante dela, sendo assim:
(-2)*(-4)*(2\sqrt{3})+(\frac{1}{2})*(1)*(\sqrt{27})+(\frac{-3}{2})*(5)*(-\sqrt{3})-[(\sqrt{27})*(-4)*(\frac{-3}{2})\\+(-\sqrt{3})*(1)*(-2)+(2\sqrt{3})*(5)*(\frac{1}{2})]\\
\ \\
simplificando\ o\ possível:\\
\ \\
16\sqrt{3}+\frac{\sqrt{27}}{2}+\frac{15\sqrt{3}}{2}-[6\sqrt{27}+2\sqrt{3}+5\sqrt{3}]Fatorando √27 temos que:
\sqrt{27}=\sqrt{3^2*3}=3\sqrt{3}Sendo assim, substituindo:
16\sqrt{3}+\frac{\sqrt{27}}{2}+\frac{15\sqrt{3}}{2}-[6\sqrt{27}+2\sqrt{3}+5\sqrt{3}]\\
\ \\
16\sqrt{3}+\frac{3\sqrt{3}}{2}+\frac{15\sqrt{3}}{2}-[6*3\sqrt{3}+2\sqrt{3}+5\sqrt{3}]\\
\ \\
16\sqrt{3}+\frac{3\sqrt{3}}{2}+\frac{15\sqrt{3}}{2}-[18\sqrt{3}+2\sqrt{3}+5\sqrt{3}]\\
\ \\
somando\ e\ subtraindo:\\
\ \\
25\sqrt{3}-25\sqrt{3}=0Como o determinante é zero temos que sim, admite inversa, logo a 02 está correta.
04.

Como queremos saber quem é B^t – A + I, primeira coisa que vamos precisar calcular é quem é a matriz B, depois a matriz B^t e por fim fazer a conta final.
Para calcular a matriz B temos o sistema dos elementos dado no enunciado, o sistema significa que:
- se i ≥ j, ou seja, diagonal principal e abaixo da diagonal principal, nós vamos somar os valores da linha e da coluna (ex: a11= 1+1=2);
- Acima da diagonal principal a conta será 2i-j (ex: a12=2*1-2=0)
Sendo assim, definimos como matriz B:
B=\left| \begin{array}{rcr}
2 & 0 & -1 \\
3 & 4& 1\\
4 & 5 & 6
\end{array} \right|Sabendo quem é a matriz B, agora vamos encontrar a transposta, invertendo linha com coluna:
B^t=\left| \begin{array}{rcr}
2 & 3 & 4 \\
0 & 4& 5\\
-1 & 1 & 6
\end{array} \right|Sabendo quem é a matriz B transposta, agora podemos fazer a soma do exercício:
B^t-A+I=\left| \begin{array}{rcr}
2 & 3 & 4 \\
0 & 4& 5\\
-1 & 1 & 6
\end{array} \right|+\left| \begin{array}{rcr}
1 & 2 & 4 \\
3 & 0& -1\\
6 & 4 & -1
\end{array} \right|+\left| \begin{array}{rcr}
1 & 0 & 0\\
0 & 1& 0\\
0 & 0 & 1
\end{array} \right|\\
\ \\
Somando\ elemento\ a\ elemento\ temos\ que:\\
\ \\
B^t-A+I=\left| \begin{array}{rcr}
2 & 1 & 0 \\
-3 & 5& 6\\
-7 & -3 & 8
\end{array} \right|Logo, como o resultado bate, a 04 está correta.
08. O sistema
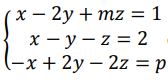
é indeterminado para 𝑚 = 2 𝑒 𝑝 = −1.
O exercício quer saber se o sistema é indeterminado, para isso ele nos da um valor de p e um valor de m.
Para identificar se um sistema de equação tem solução nós montamos a matriz dos coeficientes e calculamos o determinante deste matriz.
O p é um termo independente, logo ele é irrelevante nesta conta.
Sendo assim, montando a matriz já substituindo que m=2:
\left| \begin{array}{rcr}
1 & -2 & 2 \\
1 & -1& -1\\
-1 & 2 & -2
\end{array} \right|\\
\ \\
calculando\ o\ determinante:\\
\ \\
2-2+4-(2-2+4)=0Sendo assim como o determinante é igual a zero, este sistema não possui solução. Sendo assim a 08 está incorreta.
16. Se 𝐴 e 𝐵 são matrizes quadradas de mesma ordem, então (𝐴 ∙ 𝐵)^𝑡 = 𝐴^𝑡 ∙ 𝐵^𝑡.
A sentença 16 está incorreta. Pois a propriedade correta é:
(A.B)^t=B^t.A^t
Portanto, é uma multiplicação em ordem diferente.
32. Se 𝑥1 e 𝑥2 são raízes da equação 𝑥² + 2𝑥 + 10 = 0, então |𝑥1| + |𝑥2| = 2√10.
Logo, precisamos calcular as raízes dessa equação. Podemos fazer isso por bhaskara, logo:
x=\frac{-2\pm\sqrt{2^2-4*1*10}}{2}=\frac{-2\pm\sqrt{4-40}}{2}=\frac{-2\pm\sqrt{-36}}{2}\\
\ \\
x=\frac{-2\pm6i}{2}\\
\ \\
x1=-1+3i\\
\ \\
x2=-1-3iSomando o módulo de ambos:
|-1+3i|+|-1-3i|=-2
Logo o resultado é -2, portanto a sentença 32 está incorreta.
GABARITO 22 UFSC 2020: 13.
Confira a resolução de todos os exercícios do Enem.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.




