169 Enem 2021 – O instrumento de percussão conhecido como triângulo

169 ENEM 2021) O instrumento de percussão conhecido como triângulo é composto por uma barra fina de aço, dobrada em um formato que se assemelha a um triângulo, com uma abertura e uma haste, conforme ilustra a Figura 1.

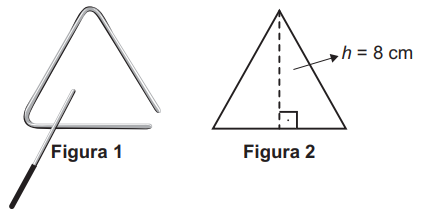
Uma empresa de brindes promocionais contrata uma fundição para a produção de miniaturas de instrumentos desse tipo.  A fundição produz, inicialmente, peças com o formato de um triângulo equilátero de altura h, conforme ilustra a Figura 2.  Após esse processo, cada peça é aquecida, deformando os cantos, e cortada em um dos vértices, dando origem à miniatura.  Assuma que não ocorram perdas de material no processo de produção, de forma que o comprimento da barra utilizada seja igual ao perímetro do triângulo equilátero representado na Figura 2.

Considere 1,7 como valor aproximado para √3.

Nessas condições, o valor que mais se aproxima da medida do comprimento da barra, em centímetro, é

a) 9,07.
b) 13,60.
c) 20,40.
d) 27,18.
e) 36,24.

Confira abaixo a resolução completa:

Solução comentada:

Temos claramente um exercício envolvendo geometria plana.

O comando deste exercício é: Nessas condições, o valor que mais se aproxima da medida do comprimento da barra, em centímetro, é .

Logo, o exercício quer saber o comprimento da barra, sabendo que o comprimento da barra é igual ao perímetro do triângulo equilátero.

Desta forma, vamos precisar descobrir qual o valor de um lado do triângulo equilátero, após isso calculamos o perímetro e temos o valor do comprimento da barra.

Para calcular o lado é simples, sabemos a altura e podemos aplicar pitágoras no triângulo, conforme a figura a seguir.

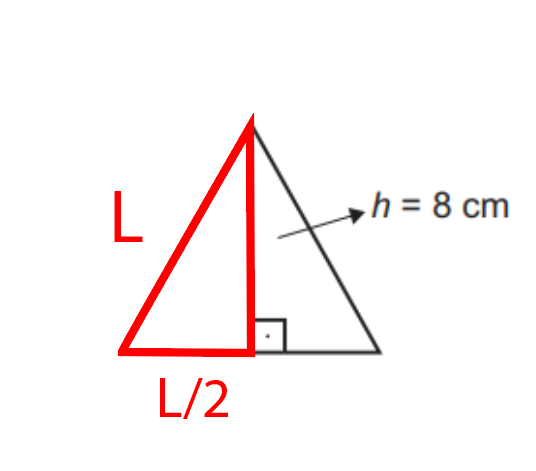
Sendo assim, por pitágoras temos que:

L^2=8^2+(\frac{L}{2})^2\\
\ \\
L^2=8^2+\frac{L^2}{4}\\
\ \\
L^2-\frac{L^2}{4}=8^2\\
\ \\
\frac{3L^2}{4}=8^2\\
\ \\
L^2=\frac{4*8^2}{3}\\
\ \\
L=\sqrt{\frac{4*8^2}{3}}\\
\ \\
L=\frac{2*8}{\sqrt{3}}\\
\ \\
L=\frac{2*8}{1,7}\\
\ \\
L=1,17*8=9,41

O perímetro é 3 vezes o lado, sendo assim:

P = 3*L=3*9,41=28,23

Logo, a alternativa que mais se aproxima disso é a alternativa D 27,18.

GABARITO 169 ENEM 2021: D.

Confira a resolução de todos os exercícios do Enem.

Confira aqui mais resoluções no site.

Quer tirar mais de 700 em Matemática no Enem?

Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:

• Muito mais organizada;
• Mais rápida;
• Economizando contas;
• Analisando os exercícios.

Adquira já o seu aqui.