35 UEPG 2018 VERÃO:
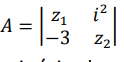
Solução comentada:
Temos claramente um exercício envolvendo números complexos, matrizes e álgebra.
Vamos para as sentenças.
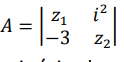
Vamos calcular então o determinante:
A=\left| \begin{array}{rcr}
z_1 & i^2 \\
-3 & z_2 \\
\end{array} \right|=z_1*z_2+3*i^2\\
\ \\
Substitundo\ os\ valores\ de\ z_1\ e\ z_2,\ além\ de\ que\ i^2=-1,\ temos:\\
\ \\
A=(1+3i)(3-9i)-3\\
\ \\
A=3-9i+9i-27i^2-3\\ \
\\
A=2727 é um número múltiplo de 3.
Sendo assim a 01 está correta.
Encontrando a parte imaginária da soma:
z_1+z_2=(1+3i)+(3-9i)=4-6i
6 não é um número primo.
Sendo assim a 02 está incorreta.
04) Se o número complexo 𝑧1 = (𝑥 + 𝑦) + (𝑥 − 𝑦)𝑖, então x + y é um divisor de 9.
Temos que z1 = (1+3i), logo:
x+y=1\\ \ \\ x-y=3
Temos que x+y = 1. E o 1 divide todos os números, logo é divisor de 9.
Sendo assim a 04 está correta.
Vamos fazer o cálculo:
\frac{z_1}{z_2}=\frac{1+3i}{3-9i}\\
\ \\
Multiplicando\ pelo\ conjugado\ para\ resolver:\\
\ \\
\frac{1+3i}{3-9i}*\frac{3-9i}{3-9i}=\frac{-24+18i}{90}Como já vemos, é um número negativo. Como nosso valor é positivo:
Sendo assim a 08 está incorreta.
Portanto o gabarito é: 01+04=5.
GABARITO 35 UEPG 2018 VERÃO: 5.
Confira a resolução de todos os exercícios do Enem.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.




