01. Na figura a seguir, 𝑟 e 𝑠 são retas paralelas
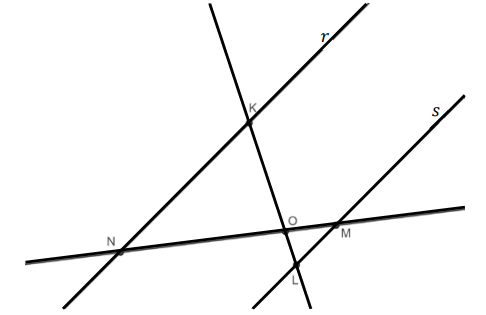
Se os segmentos 𝐿𝑂, 𝐾𝑂, 𝑁𝑂e 𝑀𝑂 medem, respectivamente, 𝑥 − 2; 5𝑥 − 14; 5𝑥 + 1; e 𝑥 + 3, então a medida do segmento 𝑀𝑁 é 28 unidades de comprimento.
02. Se num pentágono convexo as medidas dos ângulos internos são indicadas por 2𝑥, 3𝑥, 150°, 120° e 135°, então a diferença entre as medidas do maior e do menor ângulo é 130°.
04. O triângulo ABC da figura a seguir é retângulo em C; por outro lado, o triângulo AFE é
retângulo em F.
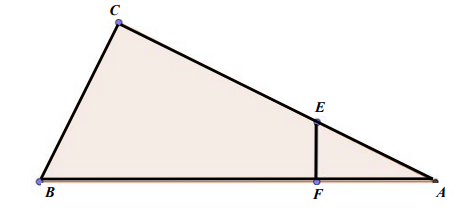
Se os segmentos 𝐴𝐶, 𝐶𝐸, 𝐴𝐹 𝑒 𝐵𝐶 medem, respectivamente, 12 𝑐𝑚, 35/4 𝑐𝑚, 𝑥 𝑐𝑚 e 5 𝑐𝑚, então a medida 𝑥 é um número racional.
08. Um hexágono cujo lado mede 4 𝑐𝑚 está inscrito numa circunferência. Se existe um quadrado circunscrito a essa circunferência, então seu perímetro mede 32 𝑐𝑚.
16. Todo losango é um paralelogramo.
32. Se os lados de um triângulo medem 8 𝑐𝑚, 10 𝑐𝑚 e 16 𝑐𝑚, então esse triângulo é acutângulo e escaleno.
64. Numa pesquisa, foi feito um levantamento entre os estudantes que usam apenas um tipo de transporte para ir à universidade. O gráfico ao lado indica a frequência obtida em cada tipo de transporte. Ocorre que, por algum problema técnico, a quantidade de respondentes que se locomovem de ônibus não apareceu na impressão do gráfico. Se a média aritmética obtida, considerando os quatro tipos de transporte, foi de 102, então a quantidade de alunos que se locomovem de ônibus é um número múltiplo de 3.
Confira abaixo a resolução completa:
Solução comentada:
01. Na figura a seguir, 𝑟 e 𝑠 são retas paralelas

Se os segmentos 𝐿𝑂, 𝐾𝑂, 𝑁𝑂e 𝑀𝑂 medem, respectivamente, 𝑥 − 2; 5𝑥 − 14; 5𝑥 + 1; e 𝑥 + 3, então a medida do segmento 𝑀𝑁 é 28 unidades de comprimento.
O exercício quer saber quem é a medida MN. Observando pelo desenho podemos dizer que MN é dado por:
MN=NO+MO\\ \ \\ onde:\\ \ \\ NO=5x+1\\ \ \\ MO=x+3\\ \ \\ sendo\ assim:\\ \ \\ MN=(5x+1)+(x+3)\\
Para encontrarmos MN precisamos saber quem é x. Podemos fazer isso através de uma semelhança de triângulos Entre os triângulos KON e LOM. Sendo assim, temos que:
\frac{KO}{LO}=\frac{NO}{MO}\\
\ \\
substituindo\ os\ valores:\\
\ \\
\frac{5x-14}{x-2}=\frac{5x+1}{x+3}\\
\ \\
(5x-14)*(x+3)=(5x+1)*(x-2)\\
\ \\
5x^2+15x-14x-42=5x^2-10x+x-2\\
\ \\
x+9x=42-2\\
\ \\
x=\frac{40}{10}=4Portanto, como x vale 4 podemos encontrar MN:
MN=(5x+1)+(x+3)\\ \ \\ MN=(5*4+1)+(4+3)\\ \ \\ MN=21+7=28
Como MN resultou em 28, a 01 está correta.
02. Se num pentágono convexo as medidas dos ângulos internos são indicadas por 2𝑥, 3𝑥, 150°, 120° e 135°, então a diferença entre as medidas do maior e do menor ângulo é 130°.
Para sabermos a diferença entre o maior e o menor ângulo, primeiramente precisamos saber qual o valor de x para identificar o menor ângulo.
Para encontrarmos o valor de x primeiro precisamos saber qual a soma dos ângulos internos deste pentágono, portanto vamos calcular através da fórmula de soma de ângulos internos de um polígono convexo:
Sn=(n-2)*180\\ \ \\ onde\ n\ é\ o\ número\ de\ lados:\\ \ \\ Sn=(5-2)*180=3*180=540\\
Sabendo que a soma total é 540, agora podemos somar todos os ângulos para encontrar x:
2x+3x+150+120+135=540\\
\ \\
5x=540-405\\
\ \\
x=\frac{135}{5}=27\\Como x vale 27 sabemos que o menor ângulo é 2x e o maior é 150, logo vamos calcular a diferença:
150-2*27=96
Como 96 é diferente de 130, a 02 está incorreta.
04. O triângulo ABC da figura a seguir é retângulo em C; por outro lado, o triângulo AFE é retângulo em F.

Se os segmentos 𝐴𝐶, 𝐶𝐸, 𝐴𝐹 𝑒 𝐵𝐶 medem, respectivamente, 12 𝑐𝑚, 35/4 𝑐𝑚, 𝑥 𝑐𝑚 e 5 𝑐𝑚, então a medida 𝑥 é um número racional.
Queremos descobrir quem é x, para isso vamos colocar todas as medidas dadas na figura:
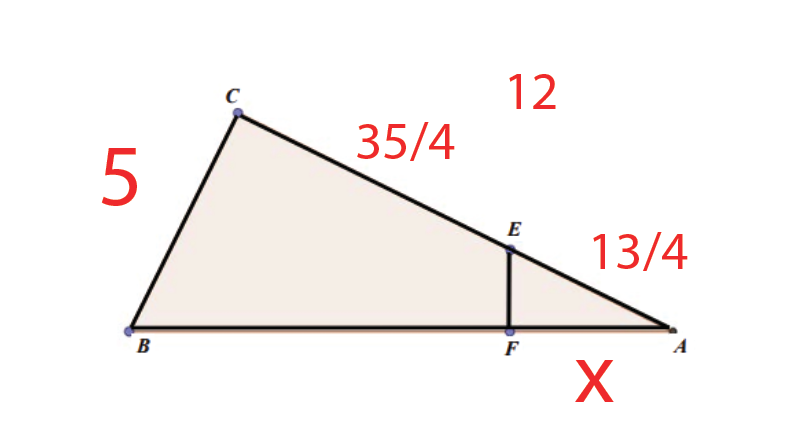
Como a medida do lado AC é 12, e a do pedaço EC é 35/4, já podemos definir que AE mede 13/4.
Para encontrarmos X precisamos saber primeiramente a medida do lado AB. Para isso, vamos fazer através de pitágoras:
BA^2=12^2+5^2\\
\ \\
BA=\sqrt{144+25}=13Sabendo o valor de BA podemos usar semelhança de triângulos para encontrar X, com os triângulos ABC e AFE. Sendo assim:
\frac{AC}{AF}=\frac{BA}{AE}\\
\ \\
\frac{12}{X}=\frac{13}{\frac{13}{4}}\\
\ \\
\frac{13}{4}*\frac{12}{13}=x\\
\ \\
3=xComo o resultado de x é 3, ele realmente é um número racional. Logo a 04 está correta.
08. Um hexágono cujo lado mede 4 𝑐𝑚 está inscrito numa circunferência. Se existe um quadrado circunscrito a essa circunferência, então seu perímetro mede 32 𝑐𝑚.
O exercício quer saber qual a medida do perímetro de um quadrado que está circunscrito (por fora) a uma circunferência, esta que tem um hexágono inscrito, no qual tem lados de 4 cm. Na figura abaixo temos essa representação.
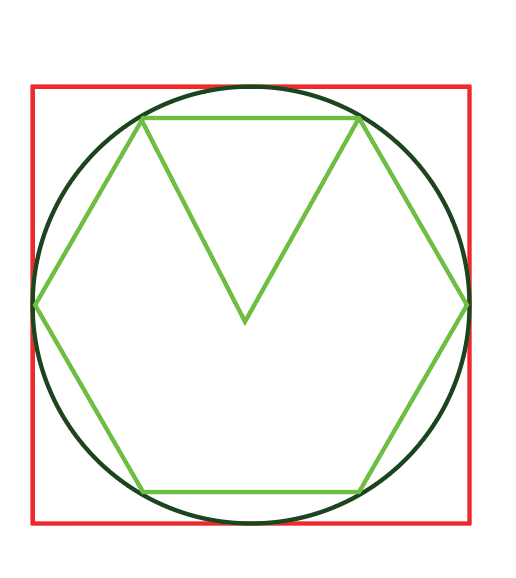
Observando a figura podemos tirar algumas conclusões:
- Diâmetro do círculo é igual ao lado do quadrado.
- Raio da circunferência é igual ao lado do hexágono, uma vez que o hexágono forma triângulos equiláteros.
Sendo assim, podemos dizer que o lado do quadrado é igual a duas vezes o lado do hexágono, logo temos que:
P=4*L=4*2*4=32
Como o perímetro realmente é 32 a sentença 08 está correta.
16. Todo losango é um paralelogramo.
Sentença 16 está correta, pois um losango tem seus lados opostos sempre paralelos, logo é um paralelogramo.
32. Se os lados de um triângulo medem 8 𝑐𝑚, 10 𝑐𝑚 e 16 𝑐𝑚, então esse triângulo é acutângulo e escaleno.
Escaleno ele é, uma vez que todos os lados são diferentes.
Para sabermos se ele é acutângulo, devemos identificar se ele possui um ângulo que é maior que 90º. Para identificarmos isso, podemos pegar os 2 menores lados e calcularmos a hipotenusa, desta forma vamos saber qual a medida de lado nos daria um ângulo de 90º. Se o valor apresentado (16) for maior, então ele não é acutângulo.
Sendo assim:
h^2=8^2+10^2\\
\ \\
h=\sqrt{64+100}\\
\ \\
h=\sqrt{164}Como sabemos que 13² é 169, logo esse valor de h é menor que 13. Como é menor que 13, é menor que 16, logo o triângulo não é acutângulo. Sendo assim a 32 está incorreta.
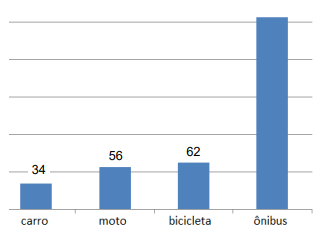
64. Numa pesquisa, foi feito um levantamento entre os estudantes que usam apenas um tipo de transporte para ir à universidade. O gráfico ao lado indica a frequência obtida em cada tipo de transporte. Ocorre que, por algum problema técnico, a quantidade de respondentes que se locomovem de ônibus não apareceu na impressão do gráfico. Se a média aritmética obtida, considerando os quatro tipos de transporte, foi de 102, então a quantidade de alunos que se locomovem de ônibus é um número múltiplo de 3.

Queremos saber a quantidade de alunos que se locomovem de ônibus. Para isso, vamos equacionar através da média e então vamos conseguir identificar se ele é múltiplo de 3:
102=\frac{34+56+62+x}{4}\\
\ \\
102*4=152+x\\
\ \\
408-152=x\\
\ \\
256=xPara sabermos se ele é múltiplo de 3 de uma forma rápida basta somarmos os 3 algarismos e verificar se esse número somado é múltiplo de 3. Se não for, o número não é;
2+5+6=13
Como 13 não é múltiplo de 3, 256 também não é, logo 64 está incorreta.
GABARITO 22 UFSC 2020: 27.
Confira a resolução de todos os exercícios do Enem.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.




